malbarbo.pro.br

6898 Algoritmos em grafos

Edição 2019/2 - Ciência da Computação

Árvores aleatórias

O objetivo deste trabalho é a implementação e teste de vários algoritmos de geração de árvores aleatórias.

O trabalho é em equipe de até três pessoas. O compartilhamento de informações entre as equipes é permitido e aconselhado, mas o compartilhamento de código não é permitido. Trabalhos que tenham porções significativas de código iguais, ou copiados da internet, serão anulados.

Descrição

Uma árvore é um grafo não orientado conexo e acíclico. Neste trabalho vamos implementar e testar três algoritmos para geração de árvores aleatórias: baseado em passeio aleatório, no algoritmo de Prim e no algoritmo de Kruskal.

Cada algoritmo recebe como entrada um número $n \gt 0$ e produz uma árvore aleatória com $n$ vértices. A seguir apresentamos o pseudocódigo dos três algoritmos:

random-tree-random-walk(n):
1  crie um grafo G com n vértices
2  for u in G.V
3      u.visitado = false
4  u = um vértice aleatório de G.V
5  u.visitado = true
5  while |G.E| < n - 1
6     v = um vértice aleatório de G.V
7     if not v.visitado
8         adicione (u, v) em G.E
9         v.visitado = true
10    u = v
11 return G

random-tree-kruskal(n):
1 crie um grafo completo G com n vértices
2 for (u, v) in G.E
3     (u, v).w = valor aleatório entre 0 e 1
4 MST-Kruskal(G, w)
5 return a árvore produzida por MST-Kruskal

random-tree-prim(n):
1 crie um grafo completo G com n vértices
2 for (u, v) in G.E
3     (u, v).w = valor aleatório entre 0 e 1
4 s = um vértice qualquer de G.V
4 MST-Prim(G, w, s)
5 return a árvore produzida por MST-Prim

A implementação de cada algoritmo deve ser testada utilizando testes automatizados. Os testes para os algoritmos determinísticos, como o MST-Kruskal e MST-Prim, devem ser escritos de forma semelhante ao que fizemos em sala para outros algoritmos: utilizando exemplos de grafos de entrada e verificando se a saída está de acordo com o esperado.

Para testar os algoritmos não determinísticos (que geram as árvores aleatórias) precisamos de outra estratégia, afinal, como verificar se uma saída é a esperada se o algoritmo é não determinístico!?

Neste caso, vamos verificar propriedades das saídas e não as saídas em si. Vamos considerar dois tipos de verificação: uma propriedade que cada saída tem que ter e uma propriedade que um conjunto de saídas tem que ter.

Uma propriedade simples que podemos verificar de cada saída é se de fato ela é uma árvore. Pode parecer simples esta verificação, mas ela é importante. Lembre-se, um dos objetivos do teste é identificar erros no código, como é plausível que um erro no código faça com que a função gere saídas que não sejam árvores é importante fazer a verificação. Como verificar se um grafo não orientado é uma árvore? Pela definição, uma árvore é grafo não orientado conexo e acíclico. Para verificar se o grafo é conexo usamos o algoritmo de busca em largura e verificamos se todos os vértices são acessíveis a partir da origem. Considerando que o grafo é conexo podemos verificar se ele é acíclico testado se o número de arestas é um a menos do que o número de vértices (você consegue entender porque esta afirmação é verdadeira?). O algoritmo a seguir verifica se uma grafo não orientado é uma árvore:

eh_arvore(G):
1 if |G.E| != |G.V| - 1
2     return False
3 s = vértice qualquer de G.V
4 BFS(G, s)
5 if se todos os vértices são acessíveis a partir de s
6     return True
7 else
8     return False

Também precisamos verificar se as árvores estão sendo geradas segundo a distribuição esperada. Neste caso não testamos uma saída apenas, mas sim se uma medida estatística de muitas saídas está de acordo com o esperado. Para este trabalho, vamos calcular a média do diâmetro das árvores. O diâmetro de uma árvore $T$ é o comprimento do maior caminho em $T$. Podemos calcular o diâmetro de uma árvore usando o algoritmo de busca em largura da seguinte maneira:

diametro(T):
1 s = vértice qualquer de T.V
2 a = o vértice com valor máximo de d obtido por BFS(T, s)
3 b = o vértice com valor máximo de d obtido por BFS(T, a)
4 return distância entre a e b

Qual é o diâmetro esperado para uma árvore gerada por cada um dos três algoritmos que vamos implementar? No algoritmo random-tree-random-walk cada árvore de $n$ vértices tem a mesma chance de ser gerada, e neste caso o diâmetro esperado é $O(\sqrt n)$ (Szekeres 1983). Já nos algoritmos random-tree-kruskal e random-tree-prim existe uma tendência de gerar árvores com diâmetros menores, neste caso, o diâmetro esperado é $O(\sqrt[3] n)$ (Addario-Berry at al. 2006).

Então, para testar os algoritmos de árvores aleatórias vamos executar cada algoritmo $500$ vezes para os valores de $n = { 250, 500, \dots 2000 }$ e verificar usando a função eh_arvore que cada saída é uma árvore. Além disso, para cada algoritmo vamos calcular o diâmetro médio das árvores para cada valor de $n$ e comparar com o valor esperado.

Para facilitar a comparação do diâmetro você pode utilizar este programa. Para executar o programa é necessário o Python 3 com as bibliotecas numpy, scipy e matplotlib. Para usar o programa você deve salvar os resultados do experimento em um arquivo como o exemplo a seguir

250 48.218
500 70.534
750 86.204
1000 100.382
1250 111.378
1500 123.114
1750 133.172
2000 142.648

A primeira coluna é o valor de $n$ e a segunda o valor médio do diâmetro das árvores geradas (para o valor de $n$ correspondente). Supondo que os resultados para o algoritmo random-tree-random-walk estejam em um arquivo chamado randomwalk.txt, o comando python3 plot.py randomwalk < randomwalk.txt vai gerar um arquivo chamado randomwalk.pdf com um gráfico semelhante a este:

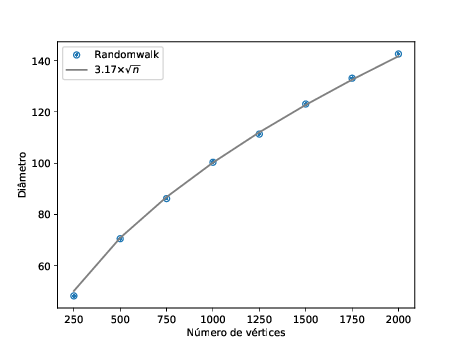
Para o algoritmo random-tree-kruskal você deve trocar o argumento randomwalk para kruskal e para o algoritmo random-tree-prim para prim.

O programa pode ser escrito em: C, C++, Java, JavaScript, Python ou Rust.

Relatório

Junto com o programa cada equipe deve entregar um relatório de no máximo 4 páginas (sem contar a capa). O relatório deve conter:

Dicas

Entrega

O trabalho deve ser entregue em etapas de acordo com o seguinte cronograma

Nos dias 14/10, 21/10, 04/11 e 11/11 o código (incluindo os testes) deve ser entregue impresso (em folha A4) na secretaria (não e necessário enviar por email). Na entrega do dia 25/11, o relatório deve ser entregue impresso em papel A4 e o diretório do programa deve ser zipado e enviado para o e-mail malbarbo arroba gmail.com. Não envie arquivos compilados, apenas os arquivos de código fonte.

Avaliação

O trabalho será avaliado de acordo com os critérios:

Referências